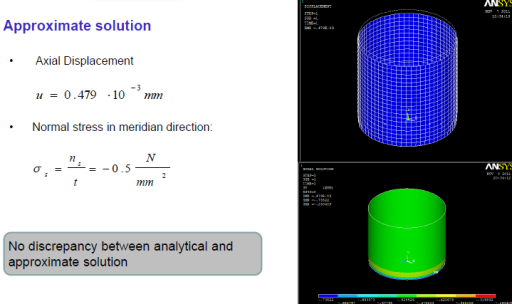
Stability Analysis of Imperfect shells
General
- Circular cylindrical shells are very stiff and light structural elements
- If a shell is loaded in such a way that the membrane energy can be converted in bending energy, it may fail dramatically.
- Very large deflections are required to transform the membrane energy to bending energy
Linear Theory
Linear Buckling Analysis
- Predicts the buckling strength of an ideal elastic structure
- The results are the buckling load factors that scale the load applied in static analysis
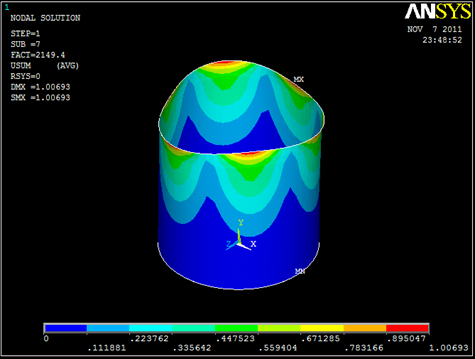
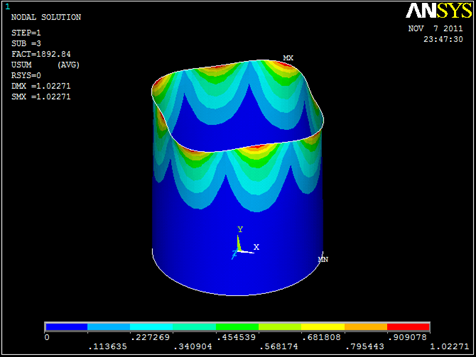
- A structure can have many buckling load factors, each of them corresponds to a deformation pattern (buckling mode shape)
- The lowest load factor is of interest
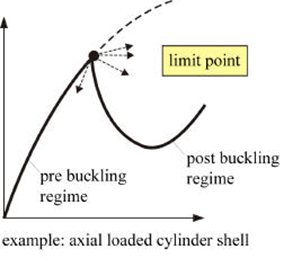
- A structure becomes unstable when a load reaches its buckling value
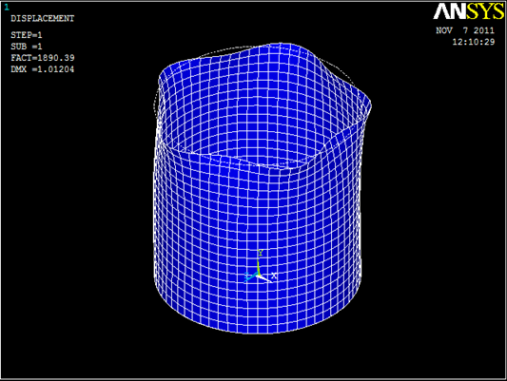
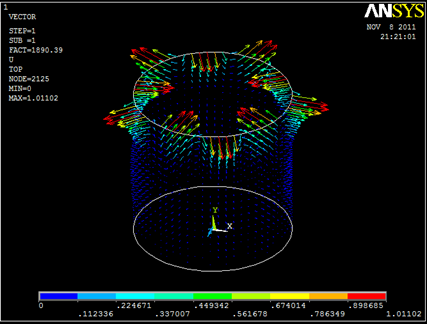
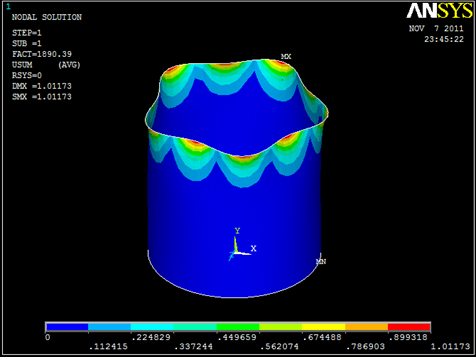
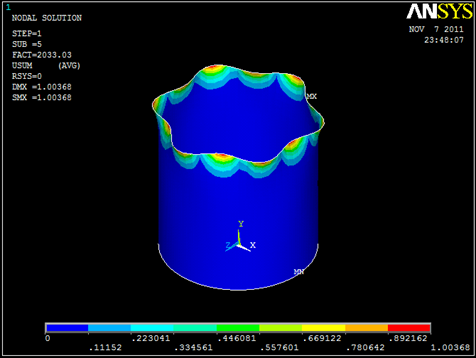
Critical load factor for the perfect system
- Pcrit = 1890.4 N/mm
Max Displacement
- u = 1.011 mm
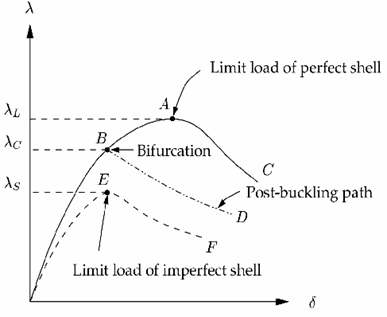
However: The critical buckling load of an imperfect shell is dramatically reduced compared to the ideal structure.
Instability Patterns for various Buckling Load Factors.
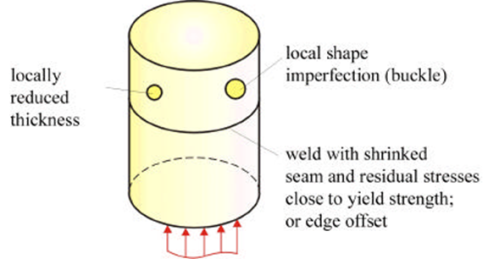
Imperfections
Linear buckling predicts the theoretical buckling strength of a perfect structure. However, non linearities reduce dramatically the buckling load.
- Geometry
- Load
- Support conditions
- Material
Non – Linear Buckling Analysis.
- More accurate approach for finding the structures limit load
- The load is increasing gradually up to the point at which the structure becomes unstable.
- Imperfections are added by updating the geometry from the linear buckling analysis
- Hence, we add the displacements of the mode shapes reduced by a scaling factor
Steps for Nonlinear Buckling Analysis
- In the first run, a convergence error occurs because the structure becomes unstable
- Inspection of the Ansys monitor file. Buckling may have started to occur if:
- The program bisects the load step increment and attempts a new solution at smaller load
- The maximum displacement has an instantaneous change in value
- The maximum displacement has an instantaneous change in sign
- We locate the corresponding time
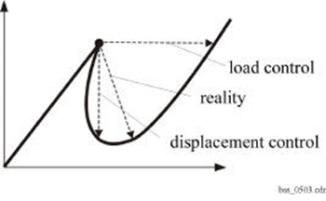
- To be sure that we have reached the critical point, we start a postbuckling analysis
- Because postbuckling analysis is unstable we apply stabilization using energy method
- We control the stabilization using energy ratios
- Higher energy ratios result in convergence but the system becomes stiffer.
- Smaller energy ratios result in no convergence.
Linear Buckling Analysis - Nonlinear Buckling Analysis
- The critical load factor from the nonlinear buckling analysis is much lower than that of the linear buckling analysis
- The cylinder buckles faster because of the geometric imperfections that were induced in the model